Alternative Data Regressor: V1
A Python Program to attain a linear regression of some alternative data against financial asset prices . A CSV file is the input. The output is the regression results.
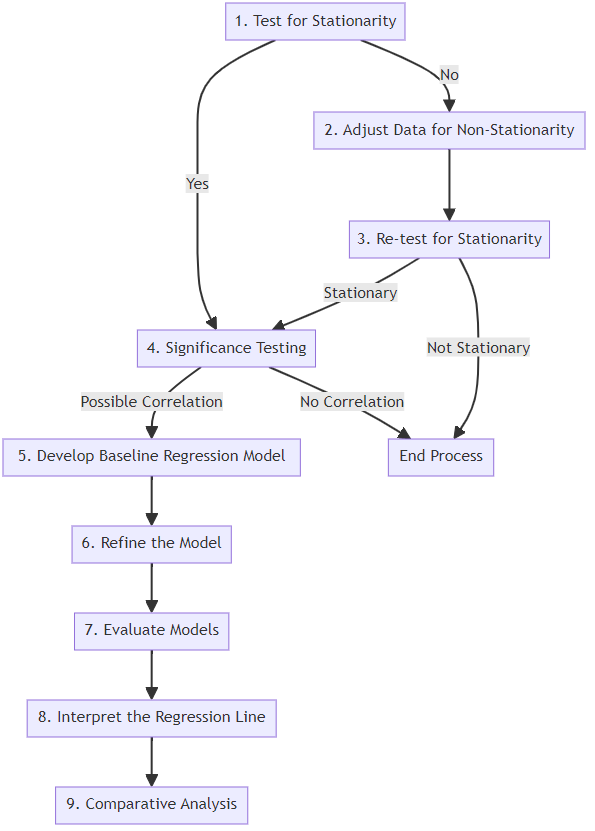
The provided Python program is designed to process time series data from a CSV file and execute a series of analytical steps based on a predefined decision tree. Key functionalities include:
Reading a CSV File: The user inputs the path to a CSV file, which the program reads into a DataFrame.
Stationarity Testing: It tests the time series data for stationarity using the Augmented Dickey-Fuller test.
Adjusting for Non-Stationarity: If the data is non-stationary, it applies a log transformation to stabilize the time series.
Re-testing for Stationarity: After transformation, it retests the data for stationarity.
Significance Testing: Conducts an Ordinary Least Squares (OLS) regression to test the significance of the relationship between the time series and a dependent variable.
Model Development and Evaluation: If a significant relationship is found, the program proceeds to develop a baseline regression model, which is then refined and evaluated based on its R-squared value.
Output: The program outputs the results of the stationarity tests, significance tests, and the R-squared value of the regression model.
import pandas as pd
import numpy as np
from statsmodels.tsa.stattools import adfuller
from statsmodels.regression.linear_model import OLS
import statsmodels.api as sm
from scipy import stats
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
def test_stationarity(timeseries):
# Perform Dickey-Fuller test:
dftest = adfuller(timeseries, autolag='AIC')
return dftest[1] # p-value
def adjust_non_stationarity(data):
# Adjusting for non-stationarity (example: log transformation)
return np.log(data)
def significance_testing(X, y):
# Perform significance testing (example: OLS regression)
X = sm.add_constant(X) # adding a constant
model = OLS(y, X).fit()
return model.pvalues
def main():
# Load data
file_path = input("Enter the path to your CSV file: ")
df = pd.read_csv(file_path)
# Assuming the time series column is named 'timeseries'
timeseries = df['timeseries']
# Step 1: Test for Stationarity
if test_stationarity(timeseries) > 0.05:
# Step 2: Adjust Data for Non-Stationarity
timeseries = adjust_non_stationarity(timeseries)
# Step 3: Re-test for Stationarity
if test_stationarity(timeseries) > 0.05:
print("Data is still non-stationary after transformation. Ending process.")
return
else:
print("Data is stationary after transformation. Proceeding with analysis.")
else:
print("Data is stationary. Proceeding with analysis.")
# Step 4: Significance Testing
# Assuming another column 'dependent_var' as the dependent variable
pvalues = significance_testing(df[['timeseries']], df['dependent_var'])
if any(pval < 0.05 for pval in pvalues[1:]): # Ignoring the constant's p-value
print("Significant correlation found. Proceeding to model development.")
else:
print("No significant correlation found. Ending process.")
return
# Steps 5, 6, 7: Develop, Refine, and Evaluate Regression Model
# This is a simplified example using OLS regression
X_train, X_test, y_train, y_test = train_test_split(df[['timeseries']], df['dependent_var'], test_size=0.2, random_state=0)
model = OLS(y_train, sm.add_constant(X_train)).fit()
predictions = model.predict(sm.add_constant(X_test))
print("Model R-squared:", r2_score(y_test, predictions))
# Step 8: Interpret the Regression Line
# This step is more analytical and depends on the specific model and data
# Step 9: Comparative Analysis
if __name__ == "__main__":
main()